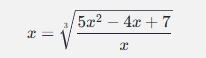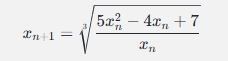A-Level 数学知识点

1. 函数变换：

解题步骤

给定点 \(P(-4, -3)\) 在曲线 \(y = f(x)\) 上。

(a) \(y = f(2x)\)

- 水平伸缩：将 \(x\) 坐标缩小为原来的 \(\frac{1}{2}\)。

\[
x' = -4 \times \frac{1}{2} = -2
\]

点映射为 \((-2, -3)\)。

(b) \(y = 3f(x - 1)\)

- 水平平移：向右平移1个单位。
- 垂直伸缩：将 \(y\) 坐标放大3倍。

水平平移：

\[
x' = -4 + 1 = -3
\]

垂直伸缩：

\[
y' = 3 \times (-3) = -9
\]

点映射为 \((-3, -9)\)。

(c) \(y = |f(x)|\)

- 绝对值函数：将 \(y\) 坐标取绝对值。

\[
y' = |-3| = 3
\]

点映射为 \((-4, 3)\)。

A-Level 数学知识点

1. 多项式函数：理解多项式的性质和根的存在性。
2. 中值定理：用于证明函数在某区间内有根。
3. 方程重构：将方程重写为不同形式。
4. 迭代法：用于近似求解方程的根。

解题步骤

(a) 证明 f(x)=0在区间$[2,3]$ 内有根

函数为：

计算 f(2) 和$f(3)$：

由于 $f(2)=-3<0$ 且 $f(3)=41>0$，根据中值定理，$f(x)$ 在 $[2,3]$ 内有根。

(b) 证明方程 $f(x)=0$ 可写为给定形式

原方程：

重构为：

两边同时开三次方根：

​​

(c) 使用迭代公式求解

迭代公式：

​​

从 x1=2x1​=2 开始：

(i) 计算 x2x2​：

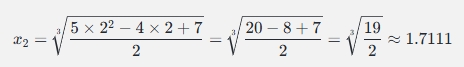
(ii) 继续迭代直到找到 $\alpha$：

继续迭代几次，直到结果稳定在四位小数。

例如：

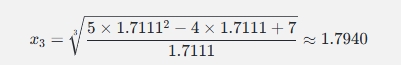
继续迭代，直到得到稳定结果，假设 $\alpha \approx 1.8171$（具体数值需要通过计算器反复迭代得出）。