A-Level 数学知识点
1. 多项式展开：将多项式乘积展开为单项式的和。
2. 不定积分：求函数的原函数。
3. 幂函数积分公式：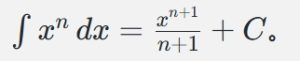
。
4. 分项积分：对多项式的每一项分别积分。
解题步骤
步骤 1: 展开多项式
首先，展开 \((2x - 5)(3x + 2)(2x + 5)\)：
1. 计算 \((3x + 2)(2x + 5)\)：
\[
(3x + 2)(2x + 5) = 3x \cdot 2x + 3x \cdot 5 + 2 \cdot 2x + 2 \cdot 5 = 6x^2 + 15x + 4x + 10 = 6x^2 + 19x + 10
\]
2. 计算 \((2x - 5)(6x^2 + 19x + 10)\)：
\[
= 2x \cdot 6x^2 + 2x \cdot 19x + 2x \cdot 10 - 5 \cdot 6x^2 - 5 \cdot 19x - 5 \cdot 10
\]
\[
= 12x^3 + 38x^2 + 20x - 30x^2 - 95x - 50
\]
\[
= 12x^3 + 8x^2 - 75x - 50
\]
步骤 2: 对每一项积分
\[
\int (12x^3 + 8x^2 - 75x - 50) \, dx
\]
1. 积分 \(12x^3\):
\[
\int 12x^3 \, dx = 12 \cdot \frac{x^4}{4} = 3x^4
\]
2. 积分 \(8x^2\):
\[
\int 8x^2 \, dx = 8 \cdot \frac{x^3}{3} = \frac{8}{3}x^3
\]
3. 积分 \(-75x\):
\[
\int -75x \, dx = -75 \cdot \frac{x^2}{2} = -\frac{75}{2}x^2
\]
4. 积分 \(-50\):
\[
\int -50 \, dx = -50x
\]
步骤 3: 合并结果
将各部分结果相加，并加上积分常数 \( C \)：
\[
3x^4 + \frac{8}{3}x^3 - \frac{75}{2}x^2 - 50x + C
\]
这就是积分的最简形式。
A-Level 数学知识点
1. 三角形面积公式：使用
计算三角形的面积。
2. 正弦定理：用于计算未知边或角。
3. 余弦定理：用于计算未知边。
解题步骤
(a) 求 \(\sin \theta\) 的值
使用三角形面积公式：
\[
\text{Area} = \frac{1}{2} \times AB \times AC \times \sin \theta
\]
已知面积为 \(100 \, \text{cm}^2\)，\(AB = 15 \, \text{cm}\)，\(AC = 25 \, \text{cm}\)，则：
\[
100 = \frac{1}{2} \times 15 \times 25 \times \sin \theta
\]
\[
100 = 187.5 \times \sin \theta
\]
\[
\sin \theta = \frac{100}{187.5} = \frac{4}{7.5}
\]
\[
\sin \theta = \frac{8}{15}
\]
(b) 求 \(BC\) 的长度
因为 \(\theta > 90^\circ\)，我们使用余弦定理：
\[
BC^2 = AB^2 + AC^2 - 2 \times AB \times AC \times \cos \theta
\]
首先计算 \(\cos \theta\)：
\[
\sin^2 \theta + \cos^2 \theta = 1
\]
\[
\cos^2 \theta = 1 - \left(\frac{8}{15}\right)^2 = 1 - \frac{64}{225} = \frac{161}{225}
\]
\[
\cos \theta = -\sqrt{\frac{161}{225}} \quad (\text{因为} \, \theta > 90^\circ)
\]
\[
\cos \theta = -\frac{\sqrt{161}}{15}
\]
代入余弦定理：
\[
BC^2 = 15^2 + 25^2 - 2 \times 15 \times 25 \times \left(-\frac{\sqrt{161}}{15}\right)
\]
\[
BC^2 = 225 + 625 + 50\sqrt{161}
\]
\[
BC = \sqrt{850 + 50\sqrt{161}}
\]
计算 \(BC\) 的近似值：
\[
BC \approx 39.1 \, \text{cm} \quad (\text{保留三位有效数字})
\]
因此，\(BC\) 的长度约为 \(39.1 \, \text{cm}\)。
感谢您选择[A-Level课程资源网]作为您的备考伙伴。我们相信，通过分享优质资源，您一定能在2024年A-level爱德思考试中脱颖而出。别忘了订阅我们的最新更新，第一时间获取更多真题和备考资料。
